IVN
0%

Blockchain_in_Go

Posted on Edited on In
Symbols count in article: 24k Reading time ≈ 21 mins.

Blockchain Proof-of-Work

A key idea of blockchain is that one has to perform some hard work to put data in it. It is this hard work that makes blockchain secure and consistent. Also, a reward is paid for this hard work (this is how people get coins for mining).

This mechanism is very similar to the one from real life: one has to work hard to get a reward and to sustain their life. In blockchain, some participants (miners) of the network work to sustain the network, to add new blocks to it, and get a reward for their work. As a result of their work, a block is incorporated into the blockchain in a secure way, which maintains the stability of the whole blockchain database. It’s worth noting that, the one who finished the work has to prove this.

This whole “do hard work and prove” mechanism is called proof-of-work. It’s hard because it requires a lot of computational power: even high performance computers cannot do it quickly. Moreover, the difficulty of this work increases from time to time to keep new blocks rate at about 6 blocks per hour. In Bitcoin, the goal of such work is to find a hash for a block, that meets some requirements. And it’s this hash that serves as a proof. Thus, finding a proof is the actual work.

One last thing to note. Proof-of-Work algorithms must meet a requirement: doing the work is hard, but verifying the proof is easy. A proof is usually handed to someone else, so for them, it shouldn’t take much time to verify it.

Hashcash

Bitcoin uses Hashcash, a Proof-of-Work algorithm that was initially developed to prevent email spam. It can be split into the following steps:

  1. Take some publicly known data (in case of email, it’s receiver’s email address; in case of Bitcoin, it’s block headers).
  2. Add a counter to it. The counter starts at 0.
  3. Get a hash of the data + counter combination.
  4. Check that the hash meets certain requirements.
    1. If it does, you’re done.
    2. If it doesn’t, increase the counter and repeat the steps 3 and 4.

Thus, this is a brute force algorithm: you change the counter, calculate a new hash, check it, increment the counter, calculate a hash, etc. That’s why it’s computationally expensive.

Now let’s look closer at the requirements a hash has to meet. In the original Hashcash implementation, the requirement sounds like “first 20 bits of a hash must be zeros”. In Bitcoin, the requirement is adjusted from time to time, because, by design, a block must be generated every 10 minutes, despite computation power increasing with time and more and more miners joining the network.

To demonstrate this algorithm, I took the data from this example (“I like donuts”) and found a hash that starts with 3 zero-bytes:

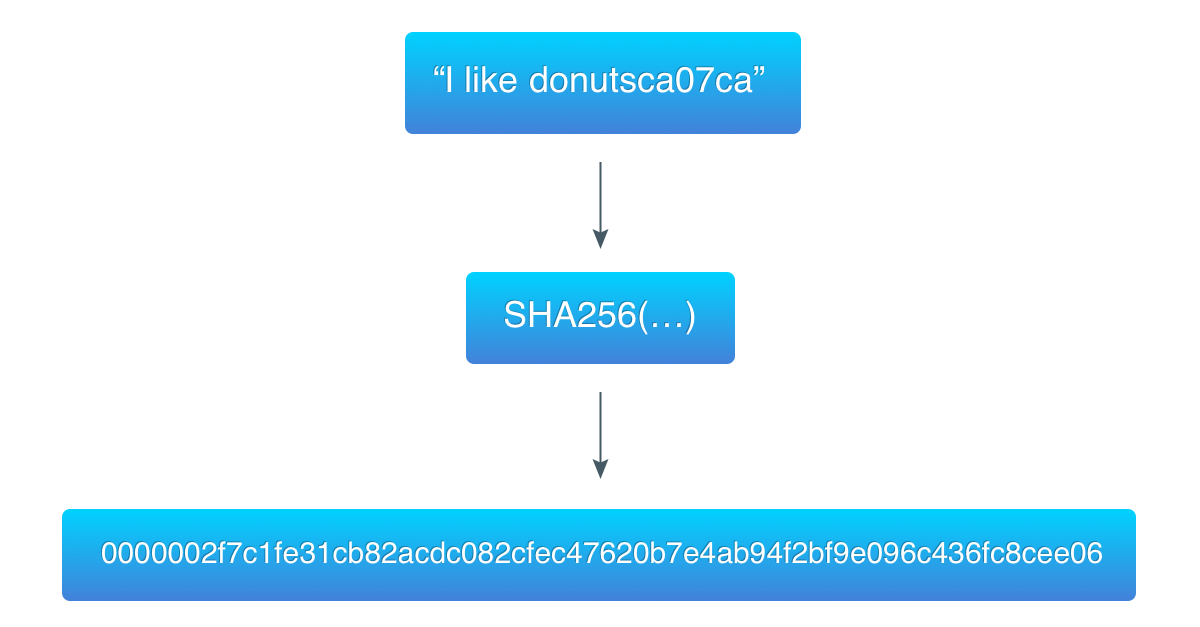
ca07ca is the hexadecimal value of the counter, which is 13240266 in the decimal system

Implementation

1
2
3
4
5
6
7
type Block struct {
	Timestamp     int64
	Data          []byte
	PrevBlockHash []byte
	Hash          []byte
	Nonce         int
}
1
2
3
4
5
6
7
8
9
10
11
12
13
type ProofOfWork struct {
	block  *Block
	target *big.Int
}

func NewProofOfWork(b *Block) *ProofOfWork {
	target := big.NewInt(1)
	target.Lsh(target, uint(256-targetBits))

	pow := &ProofOfWork{b, target}

	return pow
}

In the NewProofOfWork function, we initialize a big.Int with the value of 1 and shift it left by 256 - targetBits bits. 256 is the length of a SHA-256 hash in bits, and it’s SHA-256 hashing algorithm that we’re going to use. The hexadecimal representation of target is:

1
0x10000000000000000000000000000000000000000000000000000000000

And it occupies 29 bytes in memory. And here’s its visual comparison with the hashes from the previous examples:

1
2
3
0fac49161af82ed938add1d8725835cc123a1a87b1b196488360e58d4bfb51e3
0000010000000000000000000000000000000000000000000000000000000000
0000008b0f41ec78bab747864db66bcb9fb89920ee75f43fdaaeb5544f7f76ca

The first hash (calculated on “I like donuts”) is bigger than the target, thus it’s not a valid proof of work. The second hash (calculated on “I like donutsca07ca”) is smaller than the target, thus it’s a valid proof.

You can think of a target as the upper boundary of a range: if a number (a hash) is lower than the boundary, it’s valid, and vice versa. Lowering the boundary will result in fewer valid numbers, and thus, more difficult work required to find a valid one.

Blockchain Transactions

1
2
3
4
5
type Transaction struct {
	ID   []byte
	Vin  []TXInput
	Vout []TXOutput
}

Inputs of a new transaction reference outputs of a previous transaction (there’s an exception though, which is the first block, or genesis block). Outputs are where coins are actually stored.

Notice that:

  1. There are outputs that are not linked to inputs.
  2. In one transaction, inputs can reference outputs from multiple transactions.
  3. An input must reference an output.

TXOutput

1
2
3
4
5
6
7
8
type TXOutput struct {
    //In Bitcoin, the value field stores the number of satoshis, not the number of BTC. A satoshi is a hundred millionth of a bitcoin (0.00000001 BTC), thus this is the smallest unit of currency in Bitcoin (like a cent).
	Value        int
    
    //Internally, Bitcoin uses a scripting language called Script, that is used to define outputs locking and unlocking logic. 
	//ScriptPubKey string
    PubKeyHash []byte
}

One important thing about outputs is that they are indivisible, which means that you cannot reference a part of its value. When an output is referenced in a new transaction, it’s spent as a whole. And if its value is greater than required, a change is generated and sent back to the sender. This is similar to a real world situation when you pay, say, a $5 banknote for something that costs $1 and get a change of $4.

TXInput

1
2
3
4
5
6
7
8
9
10
11
12
type TXInput struct {
    //As mentioned earlier, an input references a previous output: Txid stores the ID of such transaction
	Txid      []byte   
    
    //Vout stores an index of an output in the transaction
	Vout      int
    
    //ScriptSig is a script which provides data to be used in an output’s ScriptPubKey. If the data is correct, the output can be unlocked, and its value can be used to generate new outputs; if it’s not correct, the output cannot be referenced in the input. This is the mechanism that guarantees that users cannot spend coins belonging to other people.
	//ScriptSig string
    Signature []byte
	PubKey    []byte
}

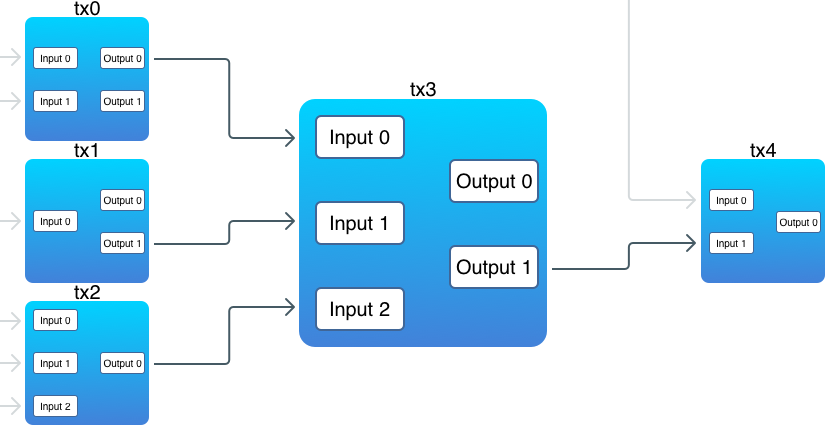
Unspent Transaction Outputs

We need to find all unspent transaction outputs (UTXO). Unspent means that these outputs weren’t referenced in any inputs. On the diagram above, these are:

  1. tx0, output 1;
  2. tx1, output 0;
  3. tx3, output 0;
  4. tx4, output 0.

How to find all UTXO that can be locked by current address?

  1. Since transactions are stored in blocks, we have to check every block in a blockchain.
  2. If an output was locked by the same address we’re searching unspent transaction outputs for, then this is the output we want. But before taking it, we need to check if an output was already referenced in an input. We skip those that were referenced in inputs (their values were moved to other outputs, thus we cannot count them).
  3. After checking outputs we gather all inputs that could unlock outputs locked with the provided address (this doesn’t apply to coinbase transactions, since they don’t unlock outputs)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
// FindUnspentTransactions returns a list of transactions containing unspent outputs
func (bc *Blockchain) FindUnspentTransactions(address string) []Transaction {
	var unspentTXs []Transaction
	spentTXOs := make(map[string][]int)
	bci := bc.Iterator()

	for {
		block := bci.Next()

        //check all tx in current block
		for _, tx := range block.Transactions {
			txID := hex.EncodeToString(tx.ID)

		Outputs:
			for outIdx, out := range tx.Vout {
				// Was the output spent?
				if spentTXOs[txID] != nil {
					for _, spentOut := range spentTXOs[txID] {
                        //skip spent output of current tx
						if spentOut == outIdx {
							continue Outputs
						}
					}
				}
				
                // If current tx contains output that can be unlocked, and this output is not spent yet, add it to unspent transactions
				if out.CanBeUnlockedWith(address) {
					unspentTXs = append(unspentTXs, *tx)
				}
			}

            
            //if not genesis block, then current tx must spent some tx before
            //mark the referenced input as spent in the previous tx 
			if tx.IsCoinbase() == false {
				for _, in := range tx.Vin {
					if in.CanUnlockOutputWith(address) {
						inTxID := hex.EncodeToString(in.Txid)
						spentTXOs[inTxID] = append(spentTXOs[inTxID], in.Vout)
					}
				}
			}
		}

		if len(block.PrevBlockHash) == 0 {
			break
		}
	}

	return unspentTXs
}

The previous function returns a list of transactions containing unspent outputs. To calculate balance we need one more function that takes the transactions and returns only outputs:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
func (bc *Blockchain) FindUTXO(address string) []TXOutput {
       var UTXOs []TXOutput
       unspentTransactions := bc.FindUnspentTransactions(address)

       for _, tx := range unspentTransactions {
               for _, out := range tx.Vout {
                       if out.CanBeUnlockedWith(address) {
                               UTXOs = append(UTXOs, out)
                       }
               }
       }

       return UTXOs
}

Sending Coins

Now, we want to send some coins to someone else. For this, we need to create a new transaction, put it in a block, and mine the block.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
func (bc *Blockchain) FindSpendableOutputs(address string, amount int) (int, map[string][]int) {
	unspentOutputs := make(map[string][]int)
	unspentTXs := bc.FindUnspentTransactions(address)
	accumulated := 0

Work:
	for _, tx := range unspentTXs {
		txID := hex.EncodeToString(tx.ID)

		for outIdx, out := range tx.Vout {
			if out.CanBeUnlockedWith(address) && accumulated < amount {
				accumulated += out.Value
				unspentOutputs[txID] = append(unspentOutputs[txID], outIdx)

                //once accumulate enough for transaction, not need to further search
				if accumulated >= amount {
					break Work
				}
			}
		}
	}

	return accumulated, unspentOutputs
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
func NewUTXOTransaction(from, to string, amount int, bc *Blockchain) *Transaction {
	var inputs []TXInput
	var outputs []TXOutput

	acc, validOutputs := bc.FindSpendableOutputs(from, amount)

	if acc < amount {
		log.Panic("ERROR: Not enough funds")
	}

	// Build a list of inputs
	for txid, outs := range validOutputs {
		txID, err := hex.DecodeString(txid)

		for _, out := range outs {
			input := TXInput{txID, out, from}
			inputs = append(inputs, input)
		}
	}

	// Build a list of outputs
    // receiver receives the coin
	outputs = append(outputs, TXOutput{amount, to})
	if acc > amount {
		outputs = append(outputs, TXOutput{acc - amount, from}) // sender receives a change, if any
	}

	tx := Transaction{nil, inputs, outputs}
	tx.SetID()

	return &tx
}

Optimization

UTXO set

As of September 18, 2017, there’re 485,860 blocks in Bitcoin and the whole database takes 140+ Gb of disk space. This means that one has to run a full node to validate transactions. Moreover, validating transactions would require iterating over many blocks.

The solution to the problem is to have an index that stores only unspent outputs, and this is what the UTXO set does: this is a cache that is built from all blockchain transactions (by iterating over blocks, yes, but this is done only once), and is later used to calculate balance and validate new transactions. The UTXO set is about 2.7 Gb as of September 2017.

Merkle Tree

As it was said above, the full Bitcoin database (i.e., blockchain) takes more than 140 Gb of disk space. Because of the decentralized nature of Bitcoin, every node in the network must be independent and self-sufficient, i.e. every node must store a full copy of the blockchain. With many people starting using Bitcoin, this rule becomes more difficult to follow: it’s not likely that everyone will run a full node. Also, since nodes are full-fledged participants of the network, they have responsibilities: they must verify transactions and blocks. Also, there’s certain internet traffic required to interact with other nodes and download new blocks.

In the original Bitcoin paper published by Satoshi Nakamoto, there was a solution for this problem: Simplified Payment Verification (SPV). SPV is a light Bitcoin node that doesn’t download the whole blockchain and doesn’t verify blocks and transactions. Instead, it finds transactions in blocks (to verify payments) and is linked to a full node to retrieve just necessary data. This mechanism allows having multiple light wallet nodes with running just one full node.

For SPV to be possible, there should be a way to check if a block contains certain transaction without downloading the whole block. And this is where Merkle tree comes into play.

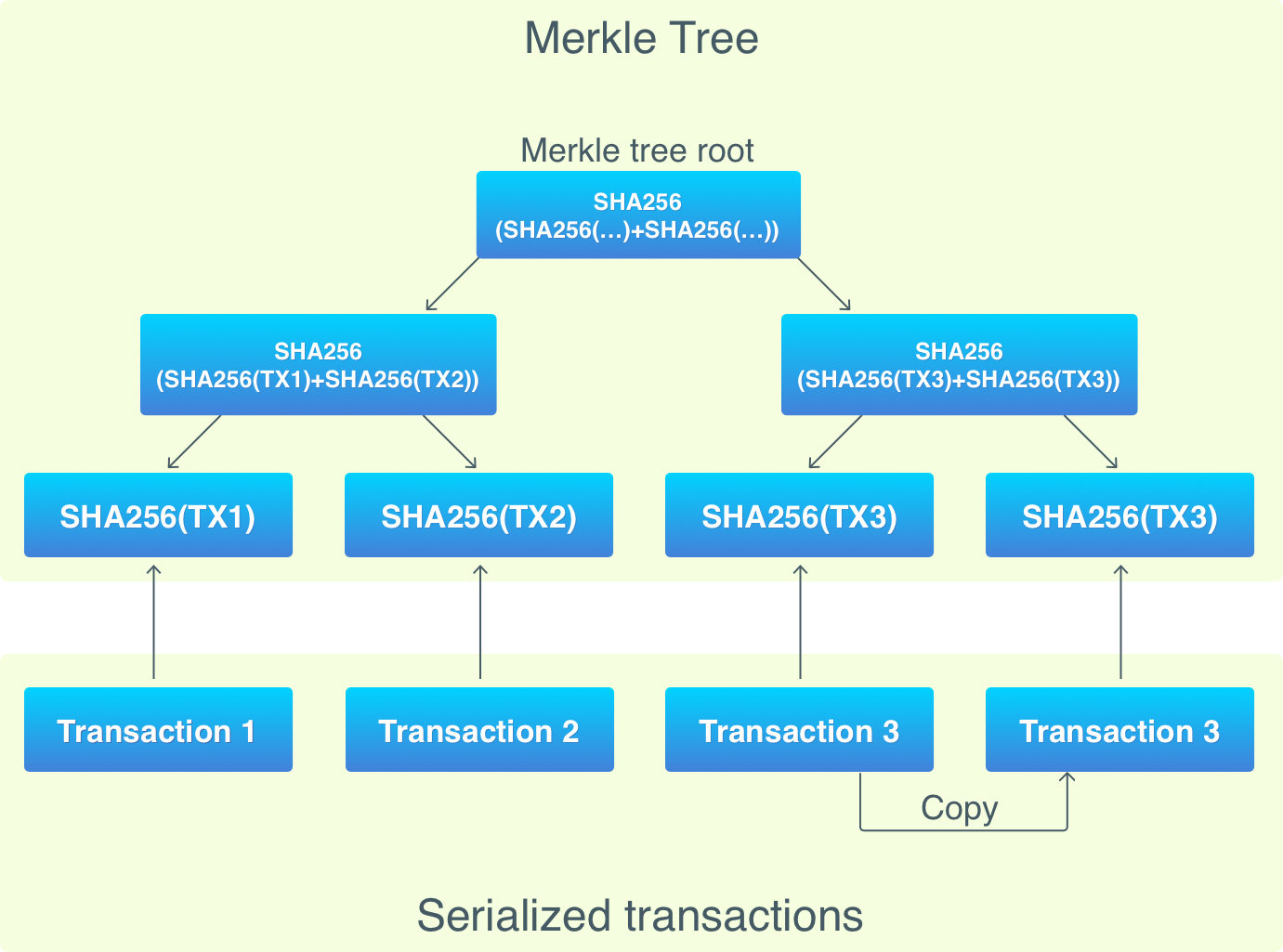
The benefit of Merkle trees is that a node can verify membership of certain transaction without downloading the whole block. Just a transaction hash, a Merkle tree root hash, and a Merkle path are required for this.

1
2
3
4
5
6
7
8
9
type MerkleTree struct {
    RootNode *MerkleNode
}

type MerkleNode struct {
    Left  *MerkleNode
    Right *MerkleNode
    Data  []byte
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
func NewMerkleNode(left, right *MerkleNode, data []byte) *MerkleNode {
    mNode := MerkleNode{}

    if left == nil && right == nil {
        hash := sha256.Sum256(data)
        mNode.Data = hash[:]
    } else {
        prevHashes := append(left.Data, right.Data...)
        hash := sha256.Sum256(prevHashes)
        mNode.Data = hash[:]
    }

    mNode.Left = left
    mNode.Right = right

    return &mNode
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
func NewMerkleTree(data [][]byte) *MerkleTree {
    var nodes []MerkleNode

    if len(data)%2 != 0 {
        data = append(data, data[len(data)-1])
    }

    for _, datum := range data {
        node := NewMerkleNode(nil, nil, datum)
        nodes = append(nodes, *node)
    }

    for i := 0; i < len(data)/2; i++ {
        var newLevel []MerkleNode

        for j := 0; j < len(nodes); j += 2 {
            node := NewMerkleNode(&nodes[j], &nodes[j+1], nil)
            newLevel = append(newLevel, *node)
        }

        nodes = newLevel
    }

    mTree := MerkleTree{&nodes[0]}

    return &mTree
}

Blockchain Addresses

Here’s an example of a Bitcoin address: 1A1zP1eP5QGefi2DMPTfTL5SLmv7DivfNa. This is the very first Bitcoin address, which allegedly belongs to Satoshi Nakamoto. Bitcoin addresses are public. If you want to send coins to someone, you need to know their address. But addresses (despite being unique) are not something that identifies you as the owner of a “wallet”. In fact, such addresses are a human readable representation of public keys. In Bitcoin, your identity is a pair (or pairs) of private and public keys stored on your computer (or stored in some other place you have access to). Bitcoin relies on a combination of cryptography algorithms to create these keys, and guarantee that no one else in the world can access your coins without getting physical access to your keys. Let’s discuss what these algorithms are.

Public-key Cryptography

Public-key cryptography algorithms use pairs of keys: public keys and private keys. Public keys are not sensitive and can be disclosed to anyone. In contrast, private keys shouldn’t be disclosed: no one but the owner should have access to them because it’s private keys that serve as the identifier of the owner. You are your private keys (in the world of cryptocurrencies, of course).

If you’ve ever used a Bitcoin wallet application, it’s likely that a mnemonic pass phrase was generated for you. Such phrases are used instead of private keys and can be used to generate them. This mechanism is implemented in BIP-039.

In essence, a Bitcoin wallet is just a pair of such keys. When you install a wallet application or use a Bitcoin client to generate a new address, a pair of keys is generated for you. The one who controls the private key controls all the coins sent to this key in Bitcoin.

Digital Signatures

In mathematics and cryptography, there’s a concept of digital signature – algorithms that guarantee:

  1. that data wasn’t modified while being transferred from a sender to a recipient;
  2. that data was created by a certain sender;
  3. that the sender cannot deny sending the data.

By applying a signing algorithm to data (i.e., signing the data), one gets a signature, which can later be verified. Digital signing happens with the usage of a private key, and verification requires a public key.

In order to sign data we need the following things:

  1. data to sign;
  2. private key.

The operation of signing produces a signature, which is stored in transaction inputs. In order to verify a signature, the following is required:

  1. data that was signed;
  2. the signature;
  3. public key.

Digital signatures are not encryption, you cannot reconstruct the data from a signature. This is similar to hashing: you run data through a hashing algorithm and get a unique representation of the data. The difference between signatures and hashes is key pairs: they make signature verification possible.
But key pairs can also be used to encrypt data: a private key is used to encrypt, and a public key is used to decrypt the data. Bitcoin doesn’t use encryption algorithms though.

Every transaction input in Bitcoin is signed by the one who created the transaction. Every transaction in Bitcoin must be verified before being put in a block. Verification means (besides other procedures):

  1. Checking that inputs have permission to use outputs from previous transactions.
  2. Checking that the transaction signature is correct.

Schematically, the process of signing data and verifying signature looks likes this:

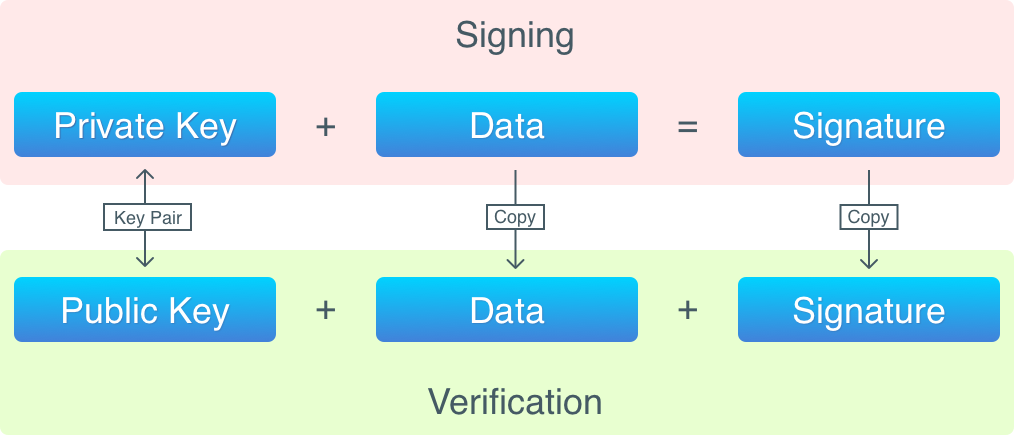
Let’s now review the full lifecycle of a transaction:

  1. In the beginning, there’s the genesis block that contains a coinbase transaction. There are no real inputs in coinbase transactions, so signing is not necessary. The output of the coinbase transaction contains a hashed public key (RIPEMD16(SHA256(PubKey)) algorithms are used).
  2. When one sends coins, a transaction is created. Inputs of the transaction will reference outputs from previous transaction(s). Every input will store a public key (not hashed) and a signature of the whole transaction.
  3. Other nodes in the Bitcoin network that receive the transaction will verify it. Besides other things, they will check that: the hash of the public key in an input matches the hash of the referenced output (this ensures that the sender spends only coins belonging to them); the signature is correct (this ensures that the transaction is created by the real owner of the coins).
  4. When a miner node is ready to mine a new block, it’ll put the transaction in a block and start mining it.
  5. When the blocked is mined, every other node in the network receives a message saying the block is mined and adds the block to the blockchain.
  6. After a block is added to the blockchain, the transaction is completed, its outputs can be referenced in new transactions.

Elliptic Curve Cryptography

As described above, public and private keys are sequences of random bytes. Since it’s private keys that are used to identify owners of coins, there’s a required condition: the randomness algorithm must produce truly random bytes. We don’t want to accidentally generate a private key that’s owned by someone else.

Bitcoin uses elliptic curves to generate private keys. Elliptic curves is a complex mathematical concept, which we’re not going to explain in details here (if you’re curious, check out this gentle introduction to elliptic curves WARNING: Math formulas!). What we need to know is that these curves can be used to generate really big and random numbers. The curve used by Bitcoin can randomly pick a number between 0 and 2²⁵⁶ (which is approximately 10⁷⁷, when there are between 10⁷⁸ and 10⁸² atoms in the visible universe). Such a huge upper limit means that it’s almost impossible to generate the same private key twice.

Also, Bitcoin uses (and we will) ECDSA (Elliptic Curve Digital Signature Algorithm) algorithm to sign transactions.

Implementing Address

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
type Wallet struct {
	PrivateKey ecdsa.PrivateKey
	PublicKey  []byte
}

type Wallets struct {
	Wallets map[string]*Wallet
}

func NewWallet() *Wallet {
	private, public := newKeyPair()
	wallet := Wallet{private, public}

	return &wallet
}

func newKeyPair() (ecdsa.PrivateKey, []byte) {
	curve := elliptic.P256()
	private, err := ecdsa.GenerateKey(curve, rand.Reader)
	pubKey := append(private.PublicKey.X.Bytes(), private.PublicKey.Y.Bytes()...)

	return *private, pubKey
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
func (w Wallet) GetAddress() []byte {
	pubKeyHash := HashPubKey(w.PublicKey)

	versionedPayload := append([]byte{version}, pubKeyHash...)
	checksum := checksum(versionedPayload)

	fullPayload := append(versionedPayload, checksum...)
	address := Base58Encode(fullPayload)

	return address
}

func HashPubKey(pubKey []byte) []byte {
	publicSHA256 := sha256.Sum256(pubKey)

	RIPEMD160Hasher := ripemd160.New()
	_, err := RIPEMD160Hasher.Write(publicSHA256[:])
	publicRIPEMD160 := RIPEMD160Hasher.Sum(nil)

	return publicRIPEMD160
}

func checksum(payload []byte) []byte {
	firstSHA := sha256.Sum256(payload)
	secondSHA := sha256.Sum256(firstSHA[:])

	return secondSHA[:addressChecksumLen]
}

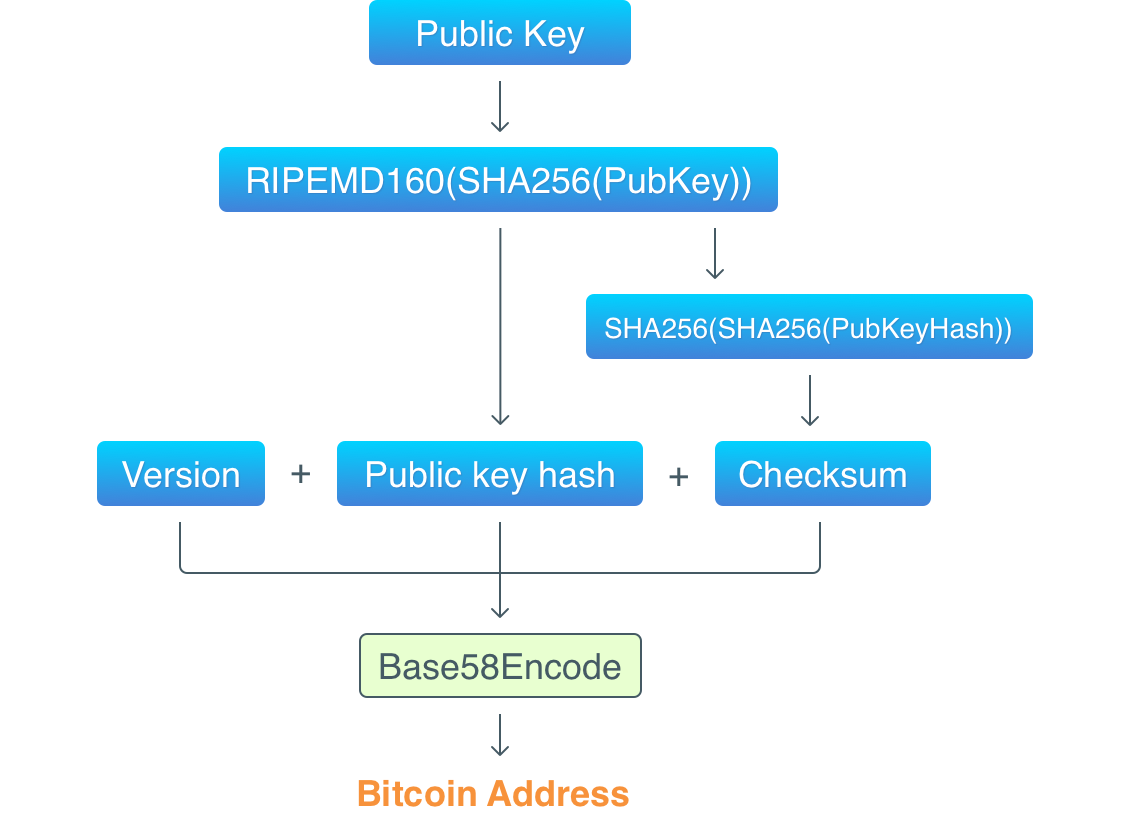
Here are the steps to convert a public key into a Base58 address:

  1. Take the public key and hash it twice with RIPEMD160(SHA256(PubKey)) hashing algorithms.

  2. Prepend the version of the address generation algorithm to the hash.

  3. Calculate the checksum by hashing the result of step 2 with SHA256(SHA256(payload)). The checksum is the first four bytes of the resulted hash.

  4. Append the checksum to the version+PubKeyHash combination.

  5. Encode the version+PubKeyHash+checksum combination with Base58.

As a result, you’ll get a real Bitcoin address, you can even check its balance on blockchain.info. But I can assure you that the balance is 0 no matter how many times you generate a new address and check its balance. This is why choosing proper public-key cryptography algorithm is so crucial: considering private keys are random numbers, the chance of generating the same number must be as low as possible. Ideally, it must be as low as “never”.

Implementing Signature

Considering that transactions unlock previous outputs, redistribute their values, and lock new outputs, the following data must be signed:

  1. Public key hashes stored in unlocked outputs. This identifies “sender” of a transaction.
  2. Public key hashes stored in new, locked, outputs. This identifies “recipient” of a transaction.
  3. Values of new outputs.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
func (tx *Transaction) Sign(privKey ecdsa.PrivateKey, prevTXs map[string]Transaction) {
	if tx.IsCoinbase() {
		return
	}

	txCopy := tx.TrimmedCopy()

	for inID, vin := range txCopy.Vin {
		prevTx := prevTXs[hex.EncodeToString(vin.Txid)]
		txCopy.Vin[inID].Signature = nil
		txCopy.Vin[inID].PubKey = prevTx.Vout[vin.Vout].PubKeyHash
		txCopy.ID = txCopy.Hash()
		txCopy.Vin[inID].PubKey = nil

		r, s, err := ecdsa.Sign(rand.Reader, &privKey, txCopy.ID)
		signature := append(r.Bytes(), s.Bytes()...)

		tx.Vin[inID].Signature = signature
	}
}

As you can see, we don’t need to sign the public keys stored in inputs. Because of this, in Bitcoin, it’s not a transaction that’s signed, but its trimmed copy with inputs storing ScriptPubKey from referenced outputs.

A detailed process of getting a trimmed transaction copy is described here. It’s likely to be outdated, but I didn’t manage to find a more reliable source of information.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
func (tx *Transaction) TrimmedCopy() Transaction {
	var inputs []TXInput
	var outputs []TXOutput

	for _, vin := range tx.Vin {
		inputs = append(inputs, TXInput{vin.Txid, vin.Vout, nil, nil})
	}

	for _, vout := range tx.Vout {
		outputs = append(outputs, TXOutput{vout.Value, vout.PubKeyHash})
	}

	txCopy := Transaction{tx.ID, inputs, outputs}

	return txCopy
}

Blockchain Network

Blockchain network is decentralized, which means there’re no servers that do stuff and clients that use servers to get or process data. In blockchain network there are nodes, and each node is a full-fledged member of the network. A node is everything: it’s both a client and a server. This is very important to keep in mind, because it’s very different from usual web applications.

Blockchain network is a P2P (Peer-to-Peer) network, which means that nodes are connected directly to each other. It’s topology is flat, since there are no hierarchy in node roles.

Node Roles

Despite being full-fledged, blockchain nodes can play different roles in the network. Here they are:

  1. Miner.
    Such nodes are run on powerful or specialized hardware (like ASIC), and their only goal is to mine new blocks as fast as possible. Miners are only possible in blockchains that use Proof-of-Work, because mining actually means solving PoW puzzles. In Proof-of-Stake blockchains, for example, there’s no mining.
  2. Full node.
    These nodes validate blocks mined by miners and verify transactions. To do this, they must have the whole copy of blockchain. Also, such nodes perform such routing operations, like helping other nodes to discover each other.
    It’s very crucial for network to have many full nodes, because it’s these nodes that make decisions: they decide if a block or transaction is valid.
  3. SPV.
    SPV stands for Simplified Payment Verification. These nodes don’t store a full copy of blockchain, but they still able to verify transactions (not all of them, but a subset, for example, those that were sent to specific address). An SPV node depends on a full node to get data from, and there could be many SPV nodes connected to one full node. SPV makes wallet applications possible: one don’t need to download full blockchain, but still can verify their transactions.

Implementation

So, what happens when you download, say, Bitcoin Core and run it for the first time? It has to connect to some node to downloaded the latest state of the blockchain. Considering that your computer is not aware of all, or some, Bitcoin nodes, what’s this node?

Hardcoding a node address in Bitcoin Core would’ve been a mistake: the node could be attacked or shut down, which could result in new nodes not being able to join the network. Instead, in Bitcoin Core, there are DNS seeds hardcoded. These are not nodes, but DNS servers that know addresses of some nodes. When you start a clean Bitcoin Core, it’ll connect to one of the seeds and get a list of full nodes, which it’ll then download the blockchain from.

In our implementation, there will be centralization though. We’ll have three nodes:

  1. The central node. This is the node all other nodes will connect to, and this is the node that’ll sends data between other nodes.
  2. A miner node. This node will store new transactions in mempool and when there’re enough of transactions, it’ll mine a new block.
  3. A wallet node. This node will be used to send coins between wallets. Unlike SPV nodes though, it’ll store a full copy of blockchain.

The Scenario

The goal of this part is to implement the following scenario:

  1. The central node creates a blockchain.
  2. Other (wallet) node connects to it and downloads the blockchain.
  3. One more (miner) node connects to the central node and downloads the blockchain.
  4. The wallet node creates a transaction.
  5. The miner nodes receives the transaction and keeps it in its memory pool.
  6. When there are enough transactions in the memory pool, the miner starts mining a new block.
  7. When a new block is mined, it’s send to the central node.
  8. The wallet node synchronizes with the central node.
  9. User of the wallet node checks that their payment was successful.